细粉加工设备(20-400目)

我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备，拥有多项国家专利，能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目，是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。

MTW系列欧版磨粉机

稀油润滑系统，新型吊挂式笼式选粉机结构设计

LM立式辊磨机

采用新型碾磨装置自动化电控系统

5X系列欧版智能磨粉机

大型规模化环保智能磨粉机优选设备

LM矿渣立式磨

LM矿渣立式磨集破碎、干燥、粉磨、分级输送于一体

立式磨煤机

烘干与制粉二合一可边磨边烘干

雷蒙磨粉机

工业磨粉设备先驱，经济实用

更多了解

超细粉加工设备(400-3250目)

LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术，专注于400-3250目范围内超细粉磨加工，细度可调可控，突破超细粉加工产能瓶颈，是超细粉加工领域粉磨装备的良好选择。

LUM超细立磨

LUM超细立磨结合现代磨粉理念

MW环辊微粉磨

采用新型碾磨装置自动化电控系统

粗粉加工设备(0-3MM)

兼具磨粉机和破碎机性能优势，产量高、破碎比大、成品率高，在粗粉加工方面成绩斐然。

LM砂粉立磨

大型效率与节能双高型砂粉制备产品

在三角形abc中ab=ac角bac=120°p为bc的中点

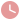
如图， ABC中，∠ BAC=120°，AB=AC，点D为BC边上的点

答案如图，作$AF\bot BC$于$F$，作$EG\bot AC$于$G$$\because \triangle ABC$中，$\angle BAC=120^ {\circ}$，$AB=AC$$\angle B=\angle C=30^ {\circ}$在$R {t}\triangle CEG$中，$\angle C=30^ {\circ}$$\therefore EG=\frac {1} {2}CE=\frac {1} 2016年11月13日如图，在 ABC中，∠BAC＝120°，P为 ABC内一点，求证：PA＋PB＋PC＞AB＋AC证明：以AC为边向外作正 ACE，则E在BA延长线上，且BE＝AB＋AC，再以AP为边作正 APQ，使B、Q位于AP两旁，连结QE在 APC与 AQE 如图，在 ABC中，∠BAC＝120°，P为 ABC内一点，求证：PA＋PB＋PC＞AB

如图,在 ABC中,∠BAC=120°,AB=AC,点M、N在边BC上,且

如图,在 ABC中,∠BAC=120°,AB=AC,点M、N在边BC上,且∠MAN=60°若BM=2,CN=4,则MN的长为 2 [分析]利用旋转作 APC,连接PC,根据旋转得: ABM≌ ACP,PC=BM=2,证明 MAN≌ PAN,则MN=PN,作高线PD,利用勾股定理计算PD和PN的长,可得结论2014年12月30日如图,在 ABC中，AB=AC，角A=120度，AB的垂直平分线MN分别交BC、AB于点M、N。求解：∵AB=AC，∠BAC=120°，∴∠B=∠C=30°，连接AM，∵MN垂直平分AB，∴AM=BM，∴∠BAM=∠B=30°，∴∠CAM=90°，∴CM=2AM∴CM=2BM 如图,在 ABC中，AB=AC，角A=120度，AB的垂直平分线MN分别交BC、AB

如图，在等腰 ABC中AB=AC，∠BAC=120°，AD⊥BC于点D，点P

2017年9月2日如图，在等腰 ABC中AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，OP与AC相交与点M，则下列结论：①点O是 PBC的外心；② MAO∽ MPC；③AC=AO+AP；④S ABC=45S四边形AOCP．其中正确的2015年1月1日在 ABC中，AB=AC=8，∠BAC=120°，取一把含30°角三角板，把30°角的顶点放在边BC的中点P处，三角板绕点在 ABC中，AB=AC=8，∠BAC=120°，取一把含30°角三角板，把30°角的顶点放在边BC的中点P处，三角板绕点P旋转．（1）如图1，当三角板的两边分别交边AB 展开分享在 ABC中，AB=AC=8，∠BAC=120°，取一把含30°角三角板

在三角形ABC中，AB=AC=8，角BAC=120度，取一把含30

2013年8月28日在三角形ABC中,AB=AC=8,角BAC=120°,取一把含30°角的三角板,把30°角的顶点放在边BC的中点M处，三角板绕点M旋转。 1）如图1，当三角形的两边分别交边AB，AC于点E，F时求证三角形BME相似于三角形CFM。如图，在 ABC中，AB=AC，∠ BAC=α ，M为BC的中点，点D在MC上，以点A为中心，将线段AD顺时针旋转α 得到线段AE，连接BE，DE (1)比较∠ BAE与∠ CAD的大小；用等式表示线段BE，BM，MD之间的数量关系，并证明；(2)过点M作AB的垂线，交DE于点N，用等式表示线段NE与ND的数量关系，并证明如图，在 ABC中，AB=AC，∠ BAC=α ，M为BC的中点，点

在三角形ABC中，角BAC=120度，以ABAC分别向形外作正

2007年9月8日举报在三角形ABC中，角BAC=120度，以ABAC分别向形外作正三角形ABD和正三角形ACE,M为AD中点怎么小学的题目也出上来了~MPN的度数~60度MPN是正三角~正三角的每个角都是60度~HOHO~以下是本人的解答本题关键是要证明MP、PN2013年4月28日小瑛拿着含30°角的透明三角板，使30°的顶点落在点P，三角板绕点P旋转。将三角板绕点p旋转成如图所示时，三角板的两条边分别交BA的延长线、边AC于点E、F设BE=x，C等腰 ABC,AB=AC=8,∠BAC=120°,P为BC的中点, 百度知道

如图，在 ABC中，∠BAC＝120°，P为 ABC内一点，求证：PA＋PB＋PC＞AB

2016年11月13日举报如图，在 ABC中，∠BAC＝120°，P为 ABC内一点，求证：PA＋PB＋PC＞AB＋AC证明：以AC为边向外作正 ACE，则E在BA延长线上，且BE＝AB＋AC，再以AP为边作正 APQ，使B、Q位于AP两旁，连结QE在 APC与 2011年10月10日取一把含30°角的三角板,把30°的角的顶点放在BC边上运动（不与BC重合） 20 在 ABC中,AB=AC=8,∠BAC=120°。取一把含30°角的三角板,把30°的角的顶点放在BC边上运动（不与BC重合）便一边经过点A，另一边与AC相交于点F（1 #热议# 网上掀起『练心眼子』风潮，真的能在 ABC中,AB=AC=8,∠BAC=120°。取一把含30°角的三角板

已知等腰三角形ABC,角BAC=120度,P为BC中点,拿着含30度

2014年3月6日已知等腰三角形ABC,角BAC=120度,P为BC中点,拿着含30度的透明三角板，使30 度角的顶点我来答首页用户认证用户帮帮团认证团队合伙人热推榜单企业媒体政府其他组织商城法律答题我的已知等腰三角形ABC,角BAC=120度,P为BC中点,拿着 2009年8月27日又BC=1/2*AB*AC*COS120°=AB*AC AB*AC=AB*AD+AC*AD 等式同时除AB*AC*AD 得1/AD=1/AB+1/AC 已赞过已踩过你对这个回答的评价是？评论收起二十加一超过23用户采纳过TA的回答知道答主回答量如图所示，在 ABC中，∠BAC=120°，AD平分∠BAC交BC于

【题文】已知：如图，在 ABC 中， AB = AC ， AB 的垂直

已知:如图,在 ABC中,AB=AC,AB的垂直平分线DE分别交AB、AC于 D、EA DE BC (1)若AC=12,BC=10,求 EBC的周长; (2)若∠A=40°,求∠EBC的度数答案 [答案] (1) EBC的周长=22; (2)∠EBC=30° [解析] [分析] (1)根据线段垂直平分线的性质可得EA=EB,进一步即可求得结果; (2)先根据等腰三角形的 2012年10月11日 ab=ac 角bac=120度所以角abc=角acb等于60度所以角edca等于30度由30度所对的边等于斜边的一半加上勾股定理即可算出ce 也可以得出ac 做垂线垂直于bc再次利用由30度所对的边等于斜边的一半加上勾股定理（或者正余弦函数）即可算出bc也就可以算出bc 最后答案等于已知如图三角形ABC中,AB=AC,角BAC=120度,DE垂直平分AC交BC于D，垂足为

2023年全国高考数学真题分类汇编大题解析版【第1章解三角

由 (1) 2023年全国高考数学真题分类汇编大题解析版【第1章解三角形合集】高清详解版13 13wenkubaidu×3 39 265 13 26×2 39 13=7 263．4 (2023 •新高考Ⅱ)记 ABC 的内角 A，B，C 的对边分别为 a，b，c，已知 ABC 面积为 3 ，D 为BC 的中点2018年3月29日如图，已知：在 ABC中，AB=AC，∠BAC=120°，P为BC边的中点，PD⊥AC．求证：CD=3AD 我来答如图，已知：在 ABC中，AB=AC，∠BAC=120°，P为BC边的中点，PD⊥AC

如图所示，在三角形ABC中，角ABC＝90度，AC=BC,D为

（1）证明：如图，连接CD，交AB于点F，AD=BD点C和点D均在线段AB的垂直平分线上直线CD为线段AB的垂直平分线为等腰直角三角形(2)如（1）中图所示若，则线段AE的长为1(1)连接CD，交AB于点F，则由线段垂直平分线的判定定理可得，直线CD是线段AB2020年3月22日下面给出了一个不同的解法 3 评论分享举报如图，在 ABC中，∠BAC=120°，AB=AC，点M、N在边BC上，MN长为多少？其实这个题目也不是奥数，初二初三，期中期末考试经常可能遇到的题目，稍微有一点难度，另一位网友的解，计算错误，下面给出了一个不同的解法如图，在 ABC中，∠BAC=120°，AB=AC，点M、N在边BC上，MN长为

如图,在三角形ABC中,AB=AC,角BAC=90度,点P为BC边上一动

2012年12月29日 P为BC中点时,三角形ACQ为直角三角形理由,AB=AC,AP=AQ,角PAQ,BAC为九十度,所以,角B,角ACB,角APQ,AQP都为45度,根据三线合一定理, 角BAP也为45度所以,AB与PQ平行又因为角B与角AQP相等所以,ABPQ为平行四边行所以,AQ平行BC又因连接CQ,所以,角AQC为直角同时,这个三角形为等腰三角形2013年1月12日如图,在等腰三角形ABC中,AB=AC,AB>BC点D在边BC上CD=2BD∵在等腰三角形ABC中，AB=AC，CD=2BD，∴ ABD与 ADC等高，底边比值为：1：2，∴ ABD与 ADC面积比为：1：2，∵ ABC的面积为9，∴ ABD与 ADC面积分别如图,在等腰三角形ABC中,AB=AC,AB>BC点D在边BC上CD=2BD

如图,在 ABC中，AB=AC，角A=120度，AB的垂直平分线MN分别交BC、AB

2014年12月30日如图,在 ABC中，AB=AC，角A=120度，AB的垂直平分线MN分别交BC、AB于点M、N。求解：∵AB=AC，∠BAC=120°，∴∠B=∠C=30°，连接AM，∵MN垂直平分AB，∴AM=BM，∴∠BAM=∠B=30°，∴∠CAM=90°，∴CM=2AM∴CM=2BM 2017年9月2日如图，在等腰 ABC中AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，OP与AC相交与点M，则下列结论：①点O是 PBC的外心；② MAO∽ MPC；③AC=AO+AP；④S ABC=45S四边形AOCP．其中正确的如图，在等腰 ABC中AB=AC，∠BAC=120°，AD⊥BC于点D，点P

在 ABC中，AB=AC=8，∠BAC=120°，取一把含30°角三角板

2015年1月1日在 ABC中，AB=AC=8，∠BAC=120°，取一把含30°角三角板，把30°角的顶点放在边BC的中点P处，三角板绕点在 ABC中，AB=AC=8，∠BAC=120°，取一把含30°角三角板，把30°角的顶点放在边BC的中点P处，三角板绕点P旋转．（1）如图1，当三角板的两边分别交边AB 展开分享 2013年8月28日在三角形ABC中,AB=AC=8,角BAC=120°,取一把含30°角的三角板,把30°角的顶点放在边BC的中点M处，三角板绕点M旋转。 1）如图1，当三角形的两边分别交边AB，AC于点E，F时求证三角形BME相似于三角形CFM。在三角形ABC中，AB=AC=8，角BAC=120度，取一把含30

如图，在 ABC中，AB=AC，∠ BAC=α ，M为BC的中点，点

如图，在 ABC中，AB=AC，∠ BAC=α ，M为BC的中点，点D在MC上，以点A为中心，将线段AD顺时针旋转α 得到线段AE，连接BE，DE (1)比较∠ BAE与∠ CAD的大小；用等式表示线段BE，BM，MD之间的数量关系，并证明；(2)过点M作AB的垂线，交DE于点N，用等式表示线段NE与ND的数量关系，并证明2007年9月8日举报在三角形ABC中，角BAC=120度，以ABAC分别向形外作正三角形ABD和正三角形ACE,M为AD中点怎么小学的题目也出上来了~MPN的度数~60度MPN是正三角~正三角的每个角都是60度~HOHO~以下是本人的解答本题关键是要证明MP、PN在三角形ABC中，角BAC=120度，以ABAC分别向形外作正

等腰 ABC,AB=AC=8,∠BAC=120°,P为BC的中点, 百度知道

2013年4月28日小瑛拿着含30°角的透明三角板，使30°的顶点落在点P，三角板绕点P旋转。将三角板绕点p旋转成如图所示时，三角板的两条边分别交BA的延长线、边AC于点E、F设BE=x，C2016年11月13日如图，在 ABC中，∠BAC＝120°，P为 ABC内一点，求证：PA＋PB＋PC＞AB＋AC证明：以AC为边向外作正 ACE，则E在BA延长线上，且BE＝AB＋AC，再以AP为边作正 APQ，使B、Q位于AP两旁，连结QE在 APC与如图，在 ABC中，∠BAC＝120°，P为 ABC内一点，求证：PA＋PB＋PC＞AB

在 ABC中,AB=AC=8,∠BAC=120°。取一把含30°角的三角板

2011年10月10日取一把含30°角的三角板,把30°的角的顶点放在BC边上运动（不与BC重合） 20 在 ABC中,AB=AC=8,∠BAC=120°。取一把含30°角的三角板,把30°的角的顶点放在BC边上运动（不与BC重合）便一边经过点A，另一边与AC相交于点F（1 #热议# 网上掀起『练心眼子』风潮，真的能

长丰下塘石头磨粉机

包装袋内原料结块碾压粉碎

抚宁磨粉机修理厂

石家庄二手鄂破机

如何制作水泥板

3010制粉设备分选

露天矿山安全监管现状调查

湿石粉干燥机

山东球磨机厂家

防沉降剂检验指标

s石头磨粉机要多少钱

博山雷蒙磨备

开石粉加工厂多少钱需要哪些手续

桂林产磨粉粉机械设备

11:1级配煤炭石子与沙的用量

超细木粉机

重庆石粉机哪里有卖

全国有规模的电厂

流体输送设备

煤层气开采需要手续

铅矿石选料设备

玄武岩磨粉加工厂

每小时产700T大口径磨粉机

广州白山研磨机六号型

生产磨粉厂的帐怎么做

废旧铝皮磨粉机

开采大理石需要什么条件

菱镁粉锤破